How AI Works: Part 3: Genetic Algorithm + Neural Network
5 comments
How Artificial Intelligence Works
Part 3: Neural Network + Genetic Algorithm
Hi Steemit! So in my previous post, we talked about how the Forward Feed Artificial Neural Network works, and I promised that I would implement one to learn using a genetic algorithm, and that I did. If you'd like to just view my spaghetti code, you can check out here. It will also be linked at the end of this post.
So now that we know the theoretical aspects of both artificial neural networks, and genetic algorithms, we're going to want to implement them! The first thing we'll need to do is implement the neural network, since without that we have nothing to teach!
(A couple of notes I'd sugget reading:
- First, some programming experience may be necessary to understand a lot of the concepts, and although the code is written in JavaScript, most of the programming concepts used are high level enough to where a basic knowledge of knowledge and Algebra is more than enough
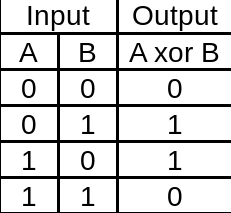
- This neural network is also built to learn to act like a XOR gate. It's a relatively programmers beginning to write AI to try and solve. The truth table for XOR is relatively simple as well.
- Remember that I'm here to help you! If you have any questions, or don't understand some parts of the code, please feel free to ask! Looking over my first two posts of this series will probably help too.)
First, we have to think on how we're going to store all of this data. The simplest way I can think of is just storing every neural network as an object in an array, which would make it relatively easy to access all the data.
We'll first start by creating a function that initializes (or puts in the first values) of the neural network array. You just put in the number of neural networks you want into the function, and it uses a for loop to push each neural network into the array. I know it sounds complicated, but it's a really simple concept. Each part of the neural network is initially random, in order to cover the widest amount of possibilities.
//Stores all nn's
var neuralNetworks = [];
//The number of neural networks that there should be at the start of each iteration. It's basically whatever number you put into init
var maxNumOfNNs = 0;
//The maximum amount that each nn can mutate
var maxMutation = 0.00001;
//The function used to squish down the output. For some reason, sigmoid doesn't work, but tanh does
var squishingFunction = "tanh";
var maxRandomForWeights = 9;
var maxRandomForBiases = 9;
function init(numOfnns) {
//Keeps the maximum number of neural networks there should be.
maxNumOfNNs = numOfnns;
for (var i = 0; i < numOfnns; i++) {
//Neural networks initialized randomly between a positive and negative maimum number
neuralNetworks.push({
//2 inputs
//4 weights
weights1: [getRandomFloat(-maxRandomForWeights, maxRandomForWeights)...],
//2 biases
biases: [getRandomFloat(-maxRandomForBiases, maxRandomForBiases)...],
//4 weights
weights2: [getRandomFloat(-maxRandomForWeights, maxRandomForWeights)...],
//1 bias
bias2: getRandomFloat(-maxRandomForBiases, maxRandomForBiases)
//1 output
});
}
}
Sweet, we've got a bunch of random neural networks. Next we're going to have to calculate their outputs based on some inputs. While I didn't go too much into the math in my neural network post, in this one we will. Don't worry, though. As long as you can do basic algebra, you should understand this fine.
function calcOutput(input1, input2, index) {
//Calculates the input of the two hidden neurons
//While this could be done all at once, I find it's easier to understand this way.
var hn1 = squish(
(input1 * neuralNetworks[index].weights1[0])
- (input2 * neuralNetworks[index].weights1[2])
- neuralNetworks[index].biases[0], squishingFunction);
var hn2 = squish( (input1 * neuralNetworks[index].weights1[1]) + (input2 * neuralNetworks[index].weights1[3]) + neuralNetworks[index].biases[1], squishingFunction);
var output = squish(hn1 * neuralNetworks[index].weights2[0] + hn2 * neuralNetworks[index].weights2[1] , squishingFunction);
return output;
}
So what does this spaghetti code do, you may be wondering. So first, the inputs (input1 and input2) are multiplied by their respective weights that connect them to the hidden neuron, then the hidden neurons' bias is added, and finally, this number is squished using either the tanh or sigmoid algorithm. This is repeated for the hidden neurons to the outputs, and finally, the output is outputted. If you need a better explanation of this, check out 3Blue1Brown's video on this.
So real quick, let's initialize the neural network with say, an initial population of 5000
//Initializes the amount of neural networks requested by the user with random weights and biases
init(5000);
Alright. So now we can finally start working on the genetic algorithm part. First, we're going to make a function that loops forever. We'll initialize some variables that will be important later, and increase the number of iterations to 1.
function cycle(){
iterations ++;
var sumCost = 0;
var outputs = [];
var costs = [];
var meanCost;
Now first, we'll want to see what every neural networks response to certain inputs are. We'll loop through every neural network, and keep it's output in an array called outputs.
//Calculate all the outputs for all the NN's and all possible inputs, and store it in the outputs array.
for (var i = 0; i < neuralNetworks.length; i++) {
outputs.push([calcOutput(0, 0, i), calcOutput(0, 1, i), calcOutput(1, 1, i), calcOutput(1, 0, i)]);
}
Next, we'll want to compare the neural network's output to the correct answer. To do this, we'll subtract our answer to the correct answer. Our goal for our neural networks is to reduce our error margin, or cost. To make sure that negative answers aren't glorified, we'll square that answer. We do that for each of all the possible inputs (there's only 4), and then find the average of those 4 errors. This is called mean square error. These will be pushed to the cost array.
//After that's done, calculate the cost using the mean squared error.
//Again, this could be done in one step, and should be for efficiency's sake, but to make it easier to understand I'm seperating the steps
for (var i = 0; i < outputs.length; i++) {
//Calculates the difference between the predicted and actual answer for XOR of 1 and 1 and squares it
//Same for all of the others
var xor00Difference = Math.pow(outputs[i][0] - 0, 2);
var xor01Difference = Math.pow(outputs[i][1] - 1, 2);
var xor11Difference = Math.pow(outputs[i][2] - 0, 2);
var xor10Difference = Math.pow(outputs[i][3] - 1, 2);
//Outputs the mean of the differences to the costs array
var output = (xor00Difference + xor01Difference + xor11Difference + xor10Difference)/4
costs.push(output);
}
This is optional, but to see how well our neural networks are doing, we'll just quickly get the average of all the costs.
//Find the sum of all of the costs
for (var i = 0; i < costs.length; i++) {
sumCost += costs[i];
}
//And divide it by the number of costs
meanCost = (sumCost/costs.length);
Great, so, we have all the errors of all of our neural networks, so how do we see which ones do best? Well the method that I decided to use was to sort all of the neural networks by how well they did (how low their costs were), and delete the bottom 75%. Basically, only the best get to survive and pass down their genes.
//Sort the arrays in descending order from least to greatest, and then let's the top x percent survive. I'm currently using 25 %
//It's like that one movie I can't remember the name of
var len = costs.length;
for (var i = len-1; i>=0; i--){
for(var j = 1; j<=i; j++){
if(costs[j-1]>costs[j]){
var temp = costs[j-1];
var temp2 = neuralNetworks[j-1];
costs[j-1] = costs[j];
costs[j] = temp;
neuralNetworks[j-1] = neuralNetworks[j];
neuralNetworks[j] = temp2;
}
}
}
neuralNetworks.splice(Math.floor(neuralNetworks.length * 0.25) )
costs.splice(Math.floor(costs.length * 0.25) )
It's pretty gruesome, but it's like real evolution, only the most fit survive. Sweet, so now we've created our neural networks, and seen how well they all do, then deleted the ones that did poorly. Now finally, we're going to want to bring the population back up. We can do this by randomly picking two AI who survived, and mixing and matching their genes. These genes are slightly mutated, to make sure that even if the AI gets stuck learning, it will eventually become better.
//First, we make sure that nobody the number of nn's has gotten lower
if (maxNumOfNNs - neuralNetworks.length > 0 && maxIterations > 0 && iterations <= maxIterations) {
for (var i = 0; i < (maxNumOfNNs - neuralNetworks.length); i++) {
var nn1 = neuralNetworks[Math.floor(Math.random() * neuralNetworks.length)];
var nn2 = neuralNetworks[Math.floor(Math.random() * neuralNetworks.length)];
neuralNetworks.push({
weights1: [ (Math.random()) > 0.5 ? nn1.weights1[0] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights1[0]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights1[1] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights1[1]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights1[2] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights1[2]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights1[3] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights1[3]+ getRandomFloat(-maxMutation, maxMutation) ],
biases: [ (Math.random()) > 0.5 ? nn1.biases[0] + getRandomFloat(-maxMutation, maxMutation) : nn2.biases[0]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.biases[1] + getRandomFloat(-maxMutation, maxMutation) : nn2.biases[1]+ getRandomFloat(-maxMutation, maxMutation) ],
weights2:[ (Math.random()) > 0.5 ? nn1.weights2[0] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights2[0]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights2[1] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights2[1]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights2[2] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights2[2]+ getRandomFloat(-maxMutation, maxMutation), (Math.random()) > 0.5 ? nn1.weights2[3] + getRandomFloat(-maxMutation, maxMutation) : nn2.weights2[3]+ getRandomFloat(-maxMutation, maxMutation) ],
bias2: (Math.random()) > 0.5 ? nn1.bias2[0] + getRandomFloat(-maxMutation, maxMutation) : nn2.bias2[0]+ getRandomFloat(-maxMutation, maxMutation)
});
}
document.getElementById('test').innerHTML = meanCost + "<p> 0 0 " + calcOutput(0, 0, 0) + "<p>" + "<p> 0 1 " + calcOutput(0, 1, 0) + "<p>" + "<p> 1 0 " + calcOutput(1, 0, 0) + "<p>" + "<p> 1 1 " + calcOutput(1, 1, 0) + "<p>" + "<p>" + iterations + "</p>";
} else {
document.getElementById('test').innerHTML = "DONE!" + "<p> 0 0 " + calcOutput(0, 0, 0) + "<p>" + "<p> 0 1 " + calcOutput(0, 1, 0) + "<p>" + "<p> 1 0 " + calcOutput(1, 0, 0) + "<p>" + "<p> 1 1 " + calcOutput(1, 1, 0) + "<p>" + "<p>" + iterations + "</p>";
}
If you've been following the code, congratulations, you just created a real and true artificial intelligence. It'll usually be able to reasonably compute XOR after just 100 iterations, and by 1000 or 10000 it's basically perfect. If you check the actual source code on the Github page, you'll see a lot of stuff about canvas and rainbows and stuff. It's not necessary at all for having the AI work, it just draws the best one to help visualize how it learns.
In our next post, we're going to get into more powerful machine learning techniques, and teaching what they are. If you want to watch this AI learn, check out here. And again, if you want to check the source code, go here and check out the XOR-Genetic-Alg.html file.
If you have any questions, feel free to let me know. Thanks!
Comments